Potenciación:
Una potencia es un producto de factores iguales. Está formada por la base y el exponente.
| Exponente | Se puede leer: tres elevado a cuatro o bien tres elevado a la cuarta | |
| 3 . 3 . 3 . 3 = 3 4 | ||
| Base |
El factor que se repite se llama base. El número de veces que se repite el factor, o sea la base, se llama exponente. Esto significa que si se tiene la potencia 2 6 (dos elevado a seis o a la sexta), la base será 2 y el exponente 6, lo cual dará como resultado 64 porque el 2 se multiplica por si mismo 6 veces (2 · 2 · 2 · 2 · 2 · 2 = 64).
Ejemplos:
2 5 = 2 • 2 • 2 • 2 • 2 = 32 El exponente es 5, esto significa que la base, el 2, se debe multiplicar por sí misma cinco veces.
3 2 = 3 • 3 = 9 El exponente es 2, esto significa que la base (3) se debe multiplicar por sí misma dos veces.
5 4 = 5 • 5 • 5 • 5 = 625 El exponente es 4, esto significa que la base (5) se debe multiplicar por sí misma cuatro veces.
Una potencia puede representarse en forma general como:
| a n = a • a • a • ........ |
Donde: a = base n = exponente “ n” factores iguales
Finalmente, recuerda que una de las aplicaciones de las potencias es la descomposición factorial de un número.
Potencia de base entera y exponente natural
Si la base a pertenece al conjunto de los Números Enteros ( a ![]() Z ) (léase a pertenece a zeta ) significa que puede tomar valores positivos y negativos . Si el exponente pertenece al conjunto de los Números Naturales , significa que puede tomar valores del uno en adelante (1, 2, 3, .....).
Z ) (léase a pertenece a zeta ) significa que puede tomar valores positivos y negativos . Si el exponente pertenece al conjunto de los Números Naturales , significa que puede tomar valores del uno en adelante (1, 2, 3, .....).
Potencia de base entera positiva:
Si la base a es positiva , la potencia siempre será un entero positivo, independiente de los valores que tome el exponente, es decir, de que sea par o impar.
| ( + a) n = + a n |
Ejemplos:
( + 4) 3 = 4 3 = 4 • 4 • 4 = 64 = + 64 Exponente impar
( + 3) 4 = 3 4 = 3 • 3 • 3 • 3 = 81 = + 81 Exponente par
Potencia de base entera negativa:
Si la base a es negativa el signo de la potencia dependerá de si el exponente es par o impar.
a) Si el exponente es par , la potencia es positiva.
| ( _ a) n (par) = + a n |
Ejemplos:
( _ 5) 2 = _ 5 • _ 5 = + 25 = 25 _ · _ = +
( _ 2) 8 = _ 2 • _ 2 • _ 2 • _ 2 • _ 2 • _ 2 • _ 2 • _ 2 = + 256 = 256
b) Si el exponente es impar , la potencia es negativa.
| ( _ a) n (impar) = _ a n |
Ejemplos:
( _ 2) 3 = _ 2 • _ 2 • _ 2 = _ 8
( _ 3) 3 = _ 3 • _ 3 • _ 3 = _ 27
En resumen:
Base | Exponente | Potencia |
Positiva | Par | Positiva |
Positiva | Impar | Positiva |
Negativa | Par | Positiva |
Negativa | Impar | Negativa |
Multiplicación de potencias de igual base
Para multiplicar potencias de igual base, se suman los exponentes y se mantiene la base.
|
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
División de potencias de igual base
Para dividir potencias de igual base, se restan los exponentes y se conserva la base.
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
Multiplicación de potencias de igual exponente
Se multiplican las bases y se conserva el exponente.
Ejemplo:
![]()
División de potencias de igual exponente
Se dividen las bases y se conserva el exponente
Ejemplo:
![]()
Potencia elevada a potencia
Se eleva la base al producto (multiplicación) de los exponentes; o sea, se conserva la base y se multiplican los exponentes.
Ejemplos:
1) ![]()
2) ![]()
Potencia de base racional y exponente entero
Sea la base ![]() (fracción) perteneciente al conjunto de los Números Racionales (
(fracción) perteneciente al conjunto de los Números Racionales ( ![]()
![]() Q ),
Q ),
donde a es el numerador y b el denominador distinto de cero, y el exponente pertenece a los números enteros (n ![]() Z). Para elevar una fracción a potencia se elevan por separado numerador y denominador.
Z). Para elevar una fracción a potencia se elevan por separado numerador y denominador.
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
Potencia de exponente negativo
Si ![]() es un número racional y – n un número entero, entonces se tiene,
es un número racional y – n un número entero, entonces se tiene,
| Si el exponente es negativo el numerador se invierte con el denominador, y el exponente cambia de signo. |
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
Propiedades de las Potencias o Leyes de los exponentes: Cuadro sinóptico |
A partir de este cuadro resumen con potencias, con ejemplos en base entera y racional, que incluye todas las propiedades, se puede resolver cualquier ejercicio de potencias.
| Propiedades | Ejemplos | ||
| Potencias de igual base | a m • a n | a m + n | 2 3 · 2 2 = 2 3 + 2 = 2 5
|
| a m : a n | a m – n |
| |
| a 0 | 1 | 23 0 = 1 | |
| (a m ) n | a m • n | ( 2 3 ) 2 = 2 3 × 2 = 2 6
| |
| Potencias de igual exponente | a m • b m | (a • b) m | 2 4 · 3 4 = (2 · 3) 4 = 6 4
|
| a m : b m | (a : b) m | 4 3 : 2 3 = (4 : 2) 3
| |
Ejercicios de aplicación de exponentes.
| = |
| = |
| = |
| = |
| = |
| = |
| = | Calcular: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Radicación Las raíces que se encuentran dentro del signo radical pueden realizar operaciones entre sí. Pueden sumarse, restarse, multiplicarse o dividirse si cumplen con determinadas condiciones o reglas. Suma y resta de radicales Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes; es decir, si son radicales con el mismo índice e igual radicando (o base subradical). (Ver: Suma y resta de radicales ) (Ver: Operaciones combinadas ) Producto o multiplicación de radicales Multiplicar radicales del mismo índice Se multiplican los radicando (las bases) y se conserva el índice
Primero se reducen a índice común y luego se multiplican. (Ver: Producto o multiplicación de radicales) Cociente o división de radicales Dividir radicales del mismo índice Se dividen los radicando (las bases) y se conserva el índice
Dividir radicales de distinto índice: Primero se reducen a índice común y luego se dividen.
Potencia de radicales
Raíz de un radical Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical.
Consiste en quitar los radicales del denominador , lo cual facilita el cálculo de operaciones como la suma de fracciones. Podemos distinguir tres casos, para eliminar los radicales del denominador. a)
.
c)
Propiedades de las raices: Debido a que las raíces pueden convertirse a potencias de exponente fraccionario, cumplen con todas las propiedades de potencias a partir de las cuales se pueden deducir las siguientes propiedades de raíces: 1) Multiplicación de raíces de igual índice:
Se multiplican las bases y se conserva el índice.
Se dividen las bases y se conserva el índice.
Para obtener raíz de raíz se multiplican los índices y se conserva la base.
Tanto el índice como el exponente de la potencia pueden amplificarse por un mismo valor.
(con la restricción que a>0 si n es par) Para introducir un factor dentro de una raíz se coloca el factor dentro del radical como potencia con exponente igual al índice y multiplicando a los demás factores. Observación: las propiedades anteriores de dan dentro de los números reales. Racionalización de fracciones con radicales. Tratándose de radicales, el proceso de racionalización consiste en eliminar las raíces que se encuentran en el denominador de una fracción. Dependiendo de las operaciones involucradas dentro de ese denominador pueden presentarse diversos casos: a) caso en que el denominador contenga una raíz cuadrada, sin adiciones ni sustracciones. Ejemplo: Racionalizar:
b) Caso en que el denominador contenga una raíz cuadrada, con adiciones o sustracciones. Ejemplo: Racionalizar: Igual que en el caso anterior, amplificamos la fracción, ahora por
Ejemplo: Racionalizar: En este caso amplificamos la fracción por
Racionalizar fracciones con radicales en el denominador sirve, entre otras aplicaciones, para ordenar de mayor a menor (para comparar) dichas fracciones. Adición y substracción de radicales Caso 1 Podemos sumar y restar radicales solamente cuando estos tengan el mismo índice y contengan una misma base (subradical o radicando). Ejemplo:
Para recordar : Como los radicales son todos iguales Veamos ahora otro ejemplo:
Como todos los términos tienen
Caso 2 ¿Podremos sumar y restar radicales que tengan el mismo índice pero que tengan distinta base? Ejemplo:
Aquí también se pide realizar una operación combinada de suma y resta. Sin embargo, no será posible porque los tres radicales poseen el mismo índice (2) y sus bases (o cantidades subradicales o radicandos) son diferentes, además de que son números primos y no se pueden factorizar . Pero, veamos otro ejemplo:
Esta también es una operación combinada de sumas y restas de radicales que tienen el mismo índice (2) pero tienen distinta base. Pero aquí hay una diferencia: las bases se pueden factorizar , de tal modo que
Simplificación de Radicales Para cumplir con las condiciones que las propiedades de los radicales les imponen a estos cuando participan en alguna operación, uno de los métodos es la simplificación de radicales . Veámoslo con diferentes ejemplos: Simplificar Un radical se puede expresar como una potencia de exponente fraccionario . Por tanto, se puede simplificar igual que una fracción; o sea, se divide el índice (12, que se coloca como denominador) y el exponente (9, que se coloca como numerador) por un mismo número. (9 y 12 son divisibles por 3, y quedan como 3 y 4)
Ahora podemos hacer el camino inverso y una potencia con exponente fraccionario como También se puede simplificar directamente (cuando es posible), dividiendo el índice y el exponente por un mismo número (12 ÷ 3 = 4 y 9 ÷ 3 = 3). Otros casos y más ejemplos: Simplificar Simplificamos directamente dividiendo, en este caso, índice y exponente entre 4. Simplificar Expresamos el radical como una potencia con exponente fraccionario y simplificamos la fracción. Simplificar Factorizamos la base (64 = 2 x 2 x 2 x 2 x 2 x 2 = 2 6 ), luego dividimos el índice (9) y el exponente (6) por 3 y desarrollamos el cuadrado de la base (4). Simplificar Factorizamos la base (81 = 3 x 3 x 3 x 3 = 3 4 ), luego dividimos el índice (8) y el exponente (4) por 2, quedando como índice 2 (que no se escribe) y la base como 3l cuyo exponente (1) tampoco se escribe. Simplificar Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical o base. Los tres radicales tienen índice 2, lo cual haciendo 2 x 2 x 2 nos da 8. La cantidad subradical o base está elevada a 8, entonces tanto el índice (8) como el exponente (8) los dividimos por 8 y queda solo la cantidad subradical o base k. Multiplicamos los índices (5 x 3 = 15) de las raíces y conservamos el exponente (10) de la base (x), luego simplificamos ambos números por 5, que divide tanto a 15 como a 10. Simplificar Expresamos el radical como una potencia con exponente fraccionario Simplificar Para dividir (o multiplicar) dos radicales ambos tienen que tener el mismo índice. En este ejemplo no es así, por lo tanto debemos reducir a un índice común, y lo hacemos igual como cuando reducimos fracciones a común denominador. En este caso, el número o índice común es el 15, el cual dividimos primero por el índice del numerador del radical (15 ÷ 5 = 3) y elevamos la base a ese exponente (3), y luego el 15 lo dividimos por el índice del radical que está como denominador (15 ÷ 3 = 5) y elevamos la base a ese exponente (5) para que la división quede
Simplificar El radical del numerador tiene índice 2 y el radical de denominador tiene índice 3. Para hacer la división debemos igualar los índices. Entre 3 y 2 el índice común es 6, lo aplicamos y operamos igual que el ejemplo anterior. Simplificar Simplificar Efectuar Sumar y simplificar Debemos recordar que para poder sumar radicales éstos tienen que tener el mismo índice y el mismo radicando. Los radicales del ejemplo tienen el mismo índice pero distinto radicando. Vamos a factorizar los radicandos (o bases) para extraer de cada sumando todos los factores posibles:
Ahora sumamos los coeficientes de cada raíz; o sea, los números que van delante de cada uno de ellos multiplicando: |
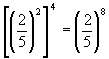
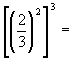
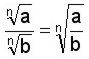
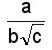
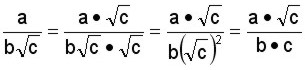
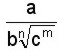
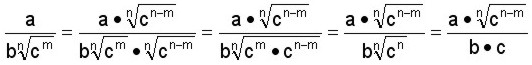
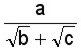
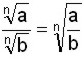
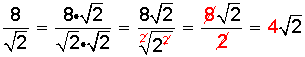
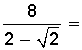
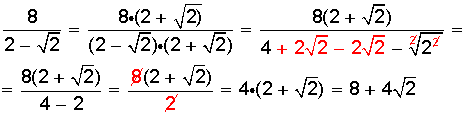
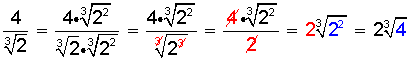
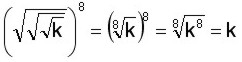
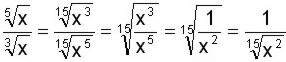
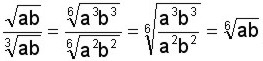
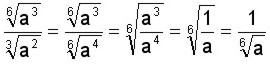
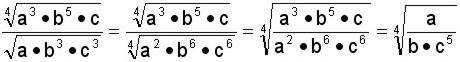
Comentarios
Publicar un comentario