Producto cartesiano, intervalos y valor absoluto.

 

Producto cartesiano y pares ordenados: definición y ejemplos

El producto cartesiano es una operación entre conjuntos muy utilizada en las matemáticas. En este artículo veremos qué son los pares ordenados, cómo se calcula el producto cartesiano y algunos ejemplos para entenderlo mejor.

Par ordenado

Habíamos visto que a la hora de expresar un conjunto no establecíamos un orden entre sus elementos. Por ello, el conjunto {a, b} era igual al {b, a}. Si necesitamos no solo expresar los elementos de un conjunto, sino también definir un orden para ellos, debemos formar un nuevo conjunto que dependa de los elementos que nos interesan y del orden en que buscamos que aparezcan.

Definición: dados dos elementos a y b, llamaremos par ordenado ab, denotado $(�,�)$ al conjunto $\{\{�\},\{�,�\}\}\mathrm{.}$ a es llamada la primera componente del par y b la segunda componente.

Puede demostrarse que $(�,�)=(�,�)$ si y solo si $�=�$ y $�=�\mathrm{.}$ Es decir, dos pares ordenados son iguales solo si sus componentes respectivas son iguales. Con la misma lógica podemos probar que $(�,�)\mathrm{\ne }(�,�)$ si y solo si $�\mathrm{\ne }�$ o $�\mathrm{\ne }�\mathrm{.}$ Es decir, dos pares son distintos si alguna de sus componentes respectivas no coinciden.

Producto cartesiano

Trabajamos anteriormente con las operaciones usuales entre conjuntos como la unión, intersección, diferencia, etc. Existe otra operación que podemos entender como una multiplicación de conjuntos, que consiste en formar un nuevo conjunto cuyos elementos sean pares ordenados con primera y segunda componente del primer y segundo conjunto respectivamente.

Definición: sean A y B dos conjuntos, producto cartesiano de A y B, denotado $�\times �$, es el conjunto cuyos elementos son todos los pares ordenados cuya primera componente pertenece a A y la segunda a B.

$�\times �=\{(�,�)\mathrm{\mid }�\in �\wedge �\in �\}$

Ejemplo: el producto cartesiano de los conjuntos $�=\{�,�,�\}$ y $�=\{1,2\}$ es el conjunto:

$A\times B=\{(a,1),(a,2),$$(�,1),(�,2),$$(�,1),(�,2)\}$

Como nos dice la definición, al producto cartesiano pertenecen todos los pares ordenados que se pueden formar con primera componente de A y segunda de B.

Algo importante a destacar es que $�\times �$ no es lo mismo que $�\times �$, hagamos la prueba:

$�\times �=\{(1,�),(1,�),$$(1,�),(2,�),$$(2,�),(2,�)\}$

Nos damos cuenta rápidamente de que $�\times �$ no es igual al conjunto $�\times �$, pues antes habíamos visto que las componentes de un par no pueden cambiarse de lugar si no son iguales. Por tanto, podemos decir que el orden en que aparecen los conjuntos es importante para calcular el producto cartesiano. 

En particular, si los conjuntos A y B son iguales, tenemos el producto cartesiano:

$�\times �={�}^2=\{(�,�)\mathrm{\mid }�\in �\wedge �\in �\}$.

Por ejemplo, con $�=\{1,2\}:$ $�\times �={�}^2=\{(1,1),(1,2),$$(2,1),(2,2)\}$

Podemos extender la definición de producto cartesiano al caso de tener tres conjuntos, en este caso también debemos extender la definición de par ordenado a terna ordenada, con tres elementos. Se sigue la misma lógica que en el caso de dos conjuntos.

Cómo calcular el producto cartesiano

Veamos algunas técnicas que podemos utilizar para facilitar el cálculo de los productos cartesianos. Esto solo servirá cuando tengamos conjuntos de pocos elementos y debamos expresar el producto por extensión. En el caso de tratar con conjuntos infinitos, dejar expresado el producto cartesiano como en la definición, es decir, por comprensión, es más que suficiente.

Producto cartesiano de 2 conjuntos

Al tratar con pares ordenados, podemos utilizar un plano con coordenadas cartesianas para representar los elementos de ambos conjuntos y hallar su producto. En el eje horizontal situamos los elementos del primer conjunto y en el eje vertical los del segundo conjunto. Luego, formamos los pares ordenados correspondientes.

Por ejemplo, sean los conjuntos $�=\{1,3\}$ y $�=\{�,�\},$ buscamos calcular $�\times �$. El gráfico cartesiano nos quedaría de la siguiente manera:

Producto cartesiano AXB

De aquí extraemos que $�\times �=\{(1,�),(1,�),(3,�),(3,�)\}\mathrm{.}$ Otra forma más compacta consiste en una tabla que sigue la misma lógica que el gráfico, como la siguiente:

c	(1, c)	(3, c)
b	(1, b)	(3, b)
$�\times �$	1	3

De aquí llegamos a los mismos pares ordenados para el producto cartesiano.

  Click aqui:  Ejercicios de productos cartesianos 💪💪

Ejercicios: 👇
1.- Dados los conjuntos :  A = {1,3,5},  B ={2,5,6},  C = {1,2,7}  y  D ={3,5,8}   Determina:  a) A X B  c)   A X D  e)   B X D  g)   B X A b) A X C  d)   B X C  f)   C X D  h)   C X B 

2.- El menú de de un restaurante ofrece: platos fuertes: pollo asado, pescado frito y ceviche de camarón, y puede acompañar su plato con arroz, ensalada o chifles. ¿Cuántas opciones distintas de almuerzos hay?. Elabora una tabla de 4x4 y elabora las opciones como producto cartesiano.

3.- 

4.- Intervalos

Intervalos

Un subconjunto de la recta real se llama intervalo, y contiene a todos los números reales que están comprendidos entre dos cualesquiera de sus elementos.

Geométricamente los intervalos corresponden a segmentos de recta, semirrectas o la misma recta real.

Los intervalos de números correspondientes a segmentos de recta son intervalos finitos, los intervalos correspondientes a semirrectas y a la recta real son intervalos infinitos.

Los intervalos finitos pueden ser cerrados, abiertos o semiabiertos.

Sean a y b dos números reales tales que a < b.

Intervalo cerrado

Es el conjunto de números reales formado por a, b y todos los comprendidos entre ambos.

[a, b] = { x / a £ x £ b}

Intervalo abierto

Es el conjunto de los números reales comprendidos entre a y b.

(a, b) = {x / a < x < b}

Intervalo semiabierto a izquierda (o semicerrado a derecha)

Es el conjunto de números reales formado por b y los números comprendidos entre a y b.

(a, b] = {x / a < x £ b}

Intervalo semiabierto a derecha (o semicerrado a izquierda)

Es el conjunto de números reales formado por a y los números comprendidos entre a y b.

[a, b) = { x / a £ x < b}

Intervalos infinitos

                      

[a, +¥) = { x / x ³ a}                                 (a, +¥) = { x / x > a}

                        

(-¥ , b] = { x / x £ b}                                 (-¥ , b) = { x / x < b}

(-¥ , +¥ ) = R

Ejemplo. Interprete gráficamente los intervalos:    a) [-2, 3]    b) (1, 4)    c) (0, 5]    d) [1, +¥ )    e) (-¥ , 3)

a) El intervalo [-2, 3] comprende todos los números reales entre -2 y 3. Como es cerrado incluye los extremos. Su representación gráfica es:

b) El intervalo (1, 4) corresponde a todos los números reales entre 1 y 4. Es abierto pues no incluye a los extremos. Gráficamente:

c) El intervalo (0, 5] comprende todos los números reales entre 0 y 5 incluyendo el extremo 5. Se trata de un intervalo semiabierto a izquierda o bien semicerrado a derecha.  Su gráfica es:

d) El intervalo [1, +¥ ) es infinito y comprende todos los números reales mayores o iguales a 1. Gráficamente:

e) El intervalo (-¥, 3) es infinito y comprende todos los números reales menores que 3. Su gráfica es:

A modo de resumen:

Nombre del intervalo	Notación conjuntista	Notación de intervalos	Representación gráfica
Abierto	{x / a < x < b}	(a, b)
Semicerrado a derecha	{x / a < x £ b}	(a, b]
Semicerrado a izquierda	{ x / a £ x < b}	[a, b)
Cerrado	{ x / a £ x £ b}	[a, b]
Infinito abierto a izquierda	{ x / x > a}	(a, +¥ )
Infinito cerrado a izquierda	{ x / x ³ a}	[a, +¥ )
Infinito abierto a derecha	{ x / x < b}	(-¥ , b)
Infinito cerrado a derecha	{ x / x £ b}	(-¥ , b]
Infinito	R	(-¥ , +¥ )

Ejemplos:

Exprese cada intervalo como una desigualdad y grafique el mismo

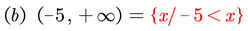
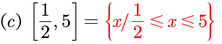
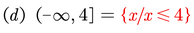
EJERCICIOS (TAREAS)

1) Escriba como intervalo el conjunto definido sobre la recta real.

a)	b)
c)	d)
e)	f)

2) Escriba, si es posible, como intervalo o unión de intervalos los siguientes conjuntos de números reales:

a) A = { x / 5 < x < 9}	b) B = { x / -1 £ x £ 3}
c) C = { x / x < -2 Ú x > 2}	d) D = { x / -4 < x < 2 Ù x ¹ -1}

3) Escriba en notación por extensión a los siguientes intervalos de números reales:

a)	b) (-¥ , -1]	c) (-7, -2]
d)	e)	f) [4, 9]

VIDEO PARA REFORZAR LA CLASE: https://youtu.be/yhdmoH_lyeU
Longitud de un intervalo: La  longitud de un intervalo (a,b), (a,b], |a,b), |a,b|; se calcula como:I= b-aEn el que el valor de b es el valor de la derecha y el valor de a es el valor de la izquierda, en la recta numérica.Ejemplos:Hallar la longitud de los intervalos:(-3,8]I=b-aI=8-(-3)=11(2,9)I=b-aI=9-2=7Centro de un intervalo: Si se cumple que a≼b, se define el centro del intervalo (a,b) como:                                                                     C= (a+b)/2Ejemplo:Hallar el número que se encuentra a la misma distancia de los extremos del intervalo (-2,7)C=(a+b)/2C= (-2+7)/2= 5/2C=2.5 unidadesRadio de un intervalo: Si se cumple que a≼b, se define el radio del intervalo (a,b) como:                                                                     r=(b-a)/2O también, una vez conocida la longitud del intervalo, su radio es la mitad de la longitud del intervalo:                                                                     r= L/2Ejemplo:Hallar el radio del intervalo semiabierto (-4,15]
r=(15-(-4))/2r= 9,5unidades
UNION E INTERSECCIÓN DE INTERVALOS

Si M y N son dos conjuntos cualesquiera, la unión de los conjuntos M y N se expresa simbólicamente así:

que es el conjunto que está formado por todos los elementos que están en M o N o en ambos.

 

La intersección de dos conjuntos P y Q, se denota

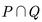
que es el conjunto de todos los elementos que están en P y Q, de otra forma es el conjunto formado por los elementos que tienen en común P y Q.

Ejemplo:

Uniones e intersecciones de intervalos

Graficar cada una de las siguientes expresiones

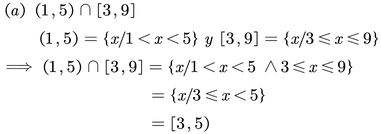
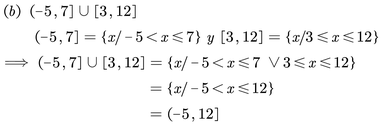Sugerencia: Además de la explicación se pueden consultar los siguientes videos  

UNION DE INTERVALOS 

https://www.youtube.com/watch?v=j-5mBl4fInA INTERSECCIÓN DE INTERVALOS https://www.youtube.com/watch?v=nx_rvu-yD70 COMPLEMENTO DE INTERVALOS https://www.youtube.com/watch?v=r6Ip60-dsJU 

DIFERENCIA DE INTERVALOS  https://www.youtube.com/watch?v=lGWCw6UUHTVALOR ABSOLUTO

 El valor absoluto es un concepto que está presente en diversos contextos de la Física y las Matemáticas, por ejemplo en las nociones de magnitud, distancia, y norma. En casos más complejos es un concepto muy útil, como en las definiciones de cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

El valor absoluto o módulo de un número real cualquiera es el mismo número pero con signo positivo. En otras palabras, es el valor numérico sin tener en cuenta su signo, ya sea positivo o negativo. Por ejemplo, el valor absoluto del número −4$-4$ se representa como |−4|$|-4|$ y equivale a 4$4$, y el valor absoluto de 4$4$ se representa como |4|$|4|$, lo cual también equivale a 4$4$.

En la recta numérica se representa como valor absoluto a la distancia que existe de un punto al origen. Por ejemplo, si se recorren 4 unidades del cero hacia la izquierda o hacia la derecha, llegamos a −4$-4$ o a 4$4$, respectivamente; el valor absoluto de cualquiera de dichos valores es 4$\mathrm{.}\mathrm{<br>}\mathrm{<br>}\mathrm{ }\mathrm{<br>}$

Formalmente, el valor absoluto de todo número real está definido por:

|a|={a,−a,sisia≥0a<0$$

$\mathrm{}$

Como podemos notar, el valor absoluto de un número real es siempre mayor que o igual a cero y nunca es negativo. Además, el valor absoluto no sólo describe la distancia de un punto al origen; de manera general, el valor absoluto puede indicar la distancia entre dos puntos cualesquiera de la recta numérica. De hecho, el concepto de función distancia o métrica en Matemáticas surge de la generalización del valor absoluto de la diferencia.

Propiedades del valor absoluto

Para poder desarrollar o entender las técnicas que se utilizan para resolver igualdades o desigualdades, es conveniente conocer las propiedades del valor absoluto. Algunas propiedades del valor absoluto derivan directamente de su definición. Por ejemplo, si tenemos un producto (o cociente) dentro de un valor absoluto como |(−3)(−2+5)|$|(-3)(-2+5)|$, el resultado se puede obtener de dos formas:

• Una es resolviendo la expresión que se encuentra encerrada entre los signos de valor absoluto (||) y posteriormente al resultado se le aplica el valor absoluto. En este caso: |(−3)(−2+5)|=|(−3)(3)|=|−9|=9$|(-3)(-2+5)|=|(-3)(3)|=|-9|=9$.
• Otra forma de resolverlo es calcular el valor absoluto de cada uno de los factores y después operarlos ya sea por producto o cociente, según sea el caso: |(−3)(−2+5)|=|(−3)(3)|=|−3||3|=9$|(-3)(-2+5)|=|(-3)(3)|=|-3||3|=9$.

Ahora consideremos los siguientes casos:

• |−43|=43$|-\frac{4}{3}|=\frac{4}{3}$
• |−43|=43$|\frac{-4}{3}|=\frac{4}{3}$
• |4−3|=43$|\frac{4}{-3}|=\frac{4}{3}$
• |43|=43$|\frac{4}{3}|=\frac{4}{3}$

Como todas son igualdades y el término de la derecha es el mismo para todas, podemos concluir que:

|−43|=|−43|=|4−3|=|−4||3|=|4||−3|$|-\frac{4}{3}|=|\frac{-4}{3}|=|\frac{4}{-3}|=\frac{|-4|}{|3|}=\frac{|4|}{|-3|}$

A partir de estos resultados vemos que podemos generalizar algunas propiedades. Dados los números reales cualesquiera a$\mathrm{ y<br><strong\; style="box-sizing:\; border-box;\; font-family:\; Arial,\; sans-serif;\; text-align:\; justify;"> </strong>}$b$\mathrm{<br>}$, se cumple que:

• |a|≥0$$
• |ab|=|a||b|$$
• |ab|=|a||b|$$
• |a+b|≤|a|+|b|$$

Otras propiedades importantes son:

• |−a|=|a|$<br>$
• |a−b|=0⇔a=b$$
• |a|≤b⇔−b≤a≤b$$
• |a|≥b⇔a≥b  ó a≤−b 
• 
  

Recuerda que el símbolo ⇔$\iff$ significa "Si y sólo si", es decir, si es cierta la proposición del lado izquierdo del símbolo, ocurre necesariamente lo del lado derecho, y si es cierta la proposición del lado derecho del símbolo, ocurre necesariamente lo del lado izquierdo.

Ejercicios:

|-5|=

|-3+2|=

|-6-4|=

|-2|+|-4|-|-8|=

|5+3|-|-2+6|+|-3+1|=

8-|3-12|+5+|7+1|=

|7-12|-|12-7|=